[Nivel:Intermedio]
Según la figura calcular el volumen del sólido limitado por el casquete esférico AN que se muestra, si el plano P es perpendicular a MN, tal que MN = 12, NB = 9 y la medida del ángulo \( \angle \)AMB es 90°
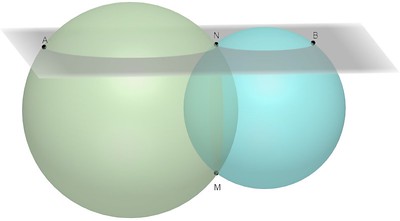
Solución
En el gráfico del problema vemos una figuras de 3 dimensiones(X,Y,Z), para hacer más sencillo la resolución del problema busquemos disminuir el número de dimensiones, en una vista frontal de la gráfica simulamos que tenemos dos dimensiones:

Si se traza una recta tangente sobre una circulo, según el gráfico:
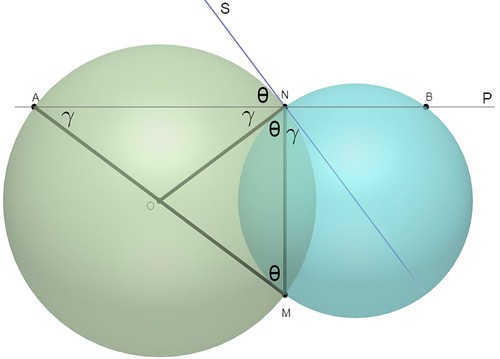
Si asumimos que:
\( \angle ANS = \theta \)
Entonces:
\( \angle AMN = \theta \)
Suponiendo que el ángulo entre la recta tangente y la recta MN es \( \gamma \)
Entonces:
\( \angle NAM = \gamma \)
Dado que \( |\overline{OA}| = |\overline{ON}| = |\overline{OM}| \)
Entonces el \( \triangle AON \) es isosceles, lo mismo que el \( \triangle NOM \)
Si ahora trazamos una recta tangente sobre el otro circulo.

Si asumimos que:
\( \angle TNB = \beta \)
Entonces:
\( \angle MNB = \beta \)
El \( \triangle NMD \) es isosceles
Por tanto:
\( \gamma = \beta \)
Por condición del problema, \( \overline{MN} \perp Plano \quad P\)
Entonces:
\( \gamma + \theta = 90° \)
Por tanto:
En el \( \triangle NMB \) el \( \angle NBM = \theta \)
Entonces:
La recta tangente al segundo circulo y \( \overline{MN} \) forman un ángulo \( \theta \)
Es decir esta recta tangente tiene la misma dirección que \( \overline{ON} \)
Luego por el enunciado,
\( |\overline{MN}| = 12\),
\( |\overline{NB}| = 9\)
\( \angle AMB = 90° \)
Quiere decir que el \( \triangle MNB \) es rectangulo y por la relación de los catetos es un triángulo notable de \( 37° \)y \( 53° \) donde \( \theta = 53° \)y \( \gamma = 37° \)
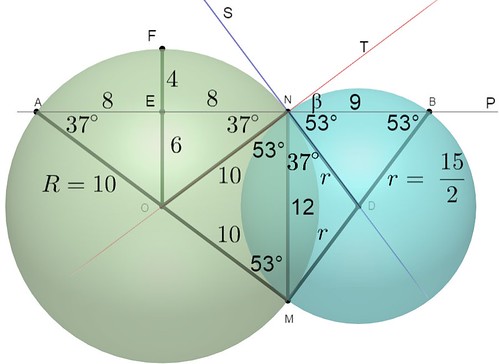
Se observa que el \( \triangle ANM \) es un triángulo rectangulo de \( 37° \)y \( 53° \) y de cateto MN igual a 12, por tanto:
\( |\overline{AN}| = 16\)
\( |\overline{AM}| = 20 \quad \therefore \quad R=10\)
Luego se traza una recta OF perpendicular a la cuerda AN, por tanto el punto E biseca a la cuerda AN.
Del triángulo rectangulo \( \triangle AEO \) de hipotenusa 10 y \( \angle OAE = 37° \) se obtiene la longitud del segmento \( |\overline{EO}| = 6\), por tanto \( |\overline{EF}| = 4\), dado que \( |\overline{OF}| = R\).
El volumen solicitado será calculado:
\( V = \cfrac{(\pi)(|\overline{EF}|)}{6}(3\times |\overline{AE}|^{2} + |\overline{EF}|^{2}) \\ V = \cfrac{(\pi)(4)}{6}(3\times 8^{2} + 4^{2}) \\ V = \cfrac{416 \pi}{3} \)
GEOMETRIA Problema 20