Problema
El número de grados x de cierto ángulo es igual a la semidiferencia entre π veces su número de grados sexagesimales y el cuádruple de su número en radianes. Entonces halle un grado x en radianes.
Bosquejo:
Graficamente en \(grados \textrm{ }Sexagesimales\textrm{ }180^o\) es:
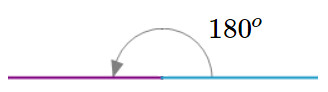
Su equivalente en \(radianes\) es \(\pi \textrm{ rad}\)
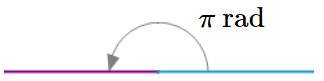
Es el mismo ángulo expresado pero en distintos sistemas de medición angular, en \( \textrm{grados sexagesimales}\) el \(número\) que representa el ángulo es \(180\), sin el \(^o\), mientras que en \(\textrm{radianes}\) el \(número\) que representa el mismo ángulo es \(3.1415...\) más conocido como \(\pi\), sin \(\textrm{rad}\).
Dado que es el mismo ángulo, cumple:
\(180^o=\pi \textrm{ rad}\)
Pero obviamente sus números son distintos:
\(180\neq\pi \)
Supongamos que tenemos un ángulo representado en el \( \textrm{sistema sexagesimal}\),\( \textrm{sistema radial}\) y \( \textrm{sistema x}\), dado que es el mismo ángulo entonces cumple:
\(S^o=R \textrm{ rad}=D^x \quad ...(i)\)
Obviamente
\(S\neq R \neq D \)
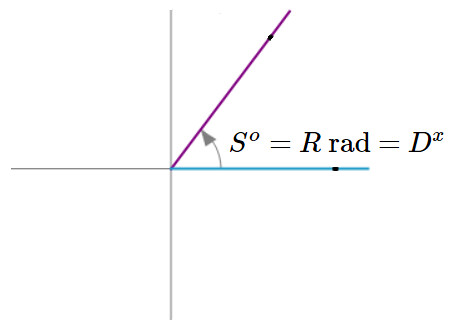
Sin embargo, sabemos que la relación de equivalencia entre los números de los distintos sistemas de medición angular es:
\( \cfrac{S}{180}=\cfrac{R}{\pi} \\ \rightarrow \quad \pi S=180R \quad ...(ii) \)
Del enunciado del problema, tenemos:
\( D = \cfrac{\pi S-4R}{2} \quad ...(iii) \)
De \((ii)\) y \((iii)\):
\( \cfrac{D}{R} = 88 ...(iii) \)
De \((i)\):
\(1^x = \cfrac{R}{D} \textrm{ rad} \quad ...(iv)\)
De \((iii)\) y \((iv)\) obtienes a cuantos radianes equivale un grado \(x\), es decir \(1^x\).